[编程笔记]-Adjacent_Difference差分

前言

差分是前缀和的逆运算，因此思想与之差不多。所以，为了更好地理解，如果有需要，请事先阅读“[编程笔记]-Partial_Sum前缀和”。

一维差分

思想及实现

同理，一维差分也可视为对差分的引入。

差分作为前缀和的逆运算，定义也与之相反。具体地说，对于数组a[]，**它的差分数组前i项之和等于a[i]**，即为a[i]=b[0]+b[1]+...+b[i]。

差分的主要作用是快速实现区间修改，若要使从l到r的区间内元素同时增加c，令b[i]=a[i]-a[i-1]，则可以使b数组第l位+c、第r+1位-c，那么从l开始，往后所有元素+c，直到第r+1位恢复原状。

上述思想十分重要，将会对后面的二维差分部分有很大帮助。

代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int n,m;
int l,r,c;
int a[N],b[N];

void insert(int l,int r,int v){
    b[l]+=v;
    b[r+1]-=v;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        insert(i,i,a[i]);//初始化b数组，视作在第i位增加a[i]大小。
    }
    while(m--){
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    for(int i=1;i<=n;i++){
        a[i]=a[i-1]+b[i];//递推实现差分
        printf("%d ",a[i]);
    }
    return 0;
}

二维差分

难点！难点！难点！

思想

初始化

首先是初始化。为了方便，我这边就直接定义我的算法中差分数组的作用了：

以原点为左上角、当前点为右下角形成矩阵，当前点的数值，就是差分数组在矩阵内的所有元素之和。

因此，当前点的数值也就是除去当前点形成的“L”型加上当前点位置上的差分数组。

鉴于该过程与前缀和中的过程基本上完全一致，只需要调转名称即可，故而就不额外配图，如有需要，前言部分中链接自取。

区间修改

然后就是区间修改部分了：

修改单点的效果

为了理解算法，我们要先理解如果修改一个点的差分值会发生什么。

已知每个点的数值与其对应的“L”型有关，又可直接视作它与原点形成的矩阵，因而一旦其矩阵中包含被修改的元素，其数值也会收到影响：

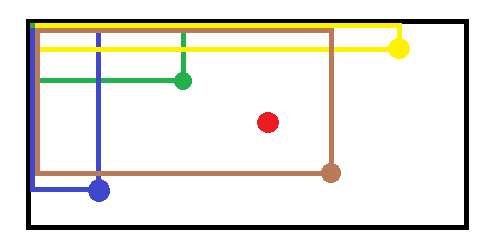
故而会受到影响的元素图如下：

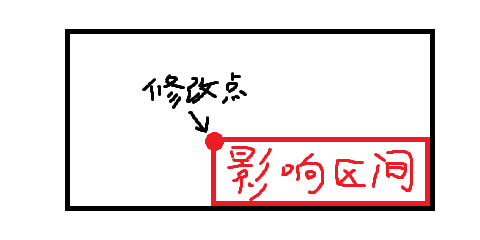
那么现在再去理解区间修改就简单多了。

步入正轨

已知受影响区间在当前点的右下角，也就是和前缀和刚好相反的，那么在此就不重复推算思路了，也就是矩阵减去“L”型。

而差分中无论是矩阵还是“L”型都在右下方，其他与前缀和基本完全一致。

如果需要详细推演过程麻烦上前言链接自取。

更新原数组

根据初始化部分中对于差分数组的定义，我们可以将原数组视作前缀和、差分数组视作前缀和中的原数组，直接代公式即可。

实现

区间修改

void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

更新原数组

a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];

代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+3;
int n,m,q;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            insert(i,j,i,j,a[i][j]);//初始化b数组
        }
    }
    int x1,y1,x2,y2,c;
    while(q--){
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];
            printf("%d ",a[i][j]);
        }
        printf("\n");
    }
    return 0;
}

完结撒花o(￣︶￣)o