[编程笔记]-Partial_Sum前缀和

一维前缀和

思想及实现

这里主要还是引入前缀和的思想，这个算法在后面还是挺常用的，可以搭配各种算法，减少时间复杂度。

前缀和呢，就是一个数组的某段前缀内的所有元素之和。举个栗子，{0,1,2,3,4,5,6}，对于这个数组，前四位的前缀和是0+1+2+3==6，前三位的前缀和是0+1+2==3。

前缀和的主要作用就是查询一段区间的元素之和。令s[i]表示a[]前i位的和，则a[i]就等于s[i]-s[i-1]。同理可推，a[l]+a[l+1]+a[l+2]+...+a[r-2]+a[r-1]+a[r]就等于s[r]-s[l-1]。

减去s[l-1]的原因：a[l]也在所需要的区间内，因此不能减去a[l]而只需减去a[l]左侧的全部元素。

通常情况下，我们会采取递推的方式预处理初前缀和，处理的复杂度是O(n)，而之后单次查询的复杂度则降到了O(1)。

代码

#include<bits/stdc++.h>
using namespace std;

const int N =1e5+5;
int a[N],s[N];
int n,m;
int l,r;

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        s[i]=s[i-1]+a[i];
    }
    while(m--){
        scanf("%d%d",&l,&r);
        printf("%d\n",s[r]-s[l-1]);
    }
    return 0;
}

二维前缀和

前言

从这里开始，我们接触的算法就开始烧脑了。

鉴于二位前缀和的复杂性（当然其实也没多复杂），我这边会搭配图片进行讲解。

思想

二位前缀和呢，若将数组视作一个矩形（左上角为原点），则前缀和储存的就是以原点为左上角、终点为右下角的矩形内包括的所有元素的和。

因此，若要求一个点的前缀和，只需求出它对应矩形缺了它这个角形成的“L”型图形内的前缀和，再加上这个点本身的数值即可。具体怎么求“L”，我将会在实现部分中写。

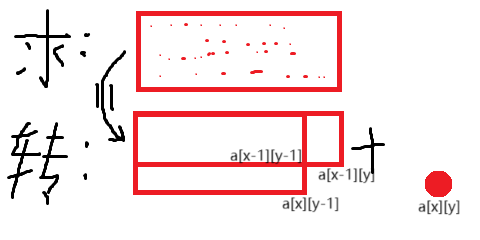
接下来就是查询的时候了：

在二维前缀和问题中，所求问题多半是一段二维区间内的元素和。循序渐进，我们从查询单个元素开始说起：

（下图中每个方格表示一个元素，实心格子表示待求元素）

其实也很简单，我们只需要把求前缀和的过程反过来就行了：用当前元素前缀和减去那个“L”型元素和即可。

延伸到一段元素，与单个元素的思路一模一样——用右下角元素的前缀和，减去包裹着整个区间的“L”型即可。

实现

不管是求前缀还是计算区间，重点就是求L型。既然我们已知当前点左侧上侧的全部前缀和，为什么不把这个复杂图形切割成我们已知的图形去做呢？

很简单，把它分成如图所示的两个前缀和，再减去它们重叠的那部分即可。

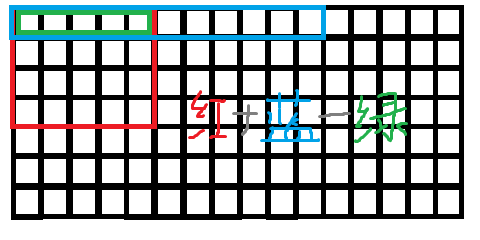
已经有了思路，下面就直接上公式了:

求前缀和：
s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j]

求[x1][y1]到[x2][y2]的元素之和:
s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]

代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+3;

int n,m,q;
int a[N][N],s[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j];
        }
    }
    int x1,y1,x2,y2;
    while(q--){
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
    }
    return 0;
}

完结撒花o(￣︶￣)o