[编程笔记]-Euler's_Totient_Function欧拉函数

概念

φ(n)表示1~n之中与n互质的数的个数

令N=P₁^α₁*P₂^α₂*P₃^α₃*…*P_k^α_k

则φ(N)=N(1-1/P₁)(1-1/P₂)(1-1/P₃)…(1-1/P_k)

推导

1. 求出N的质因数
2. 从1~N中去掉P₁，P₂到P_k的倍数。
3. 加上所有P_i*P_j的倍数，因为第二步把它们多减了一次。
4. 减去所有P_i*P_j*P_k的倍数，因为第三步把它们多加了一次……

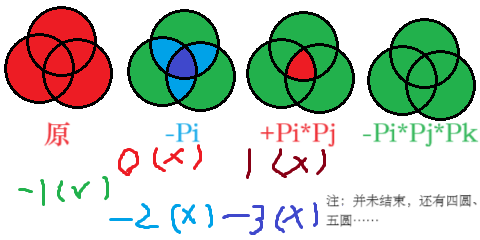
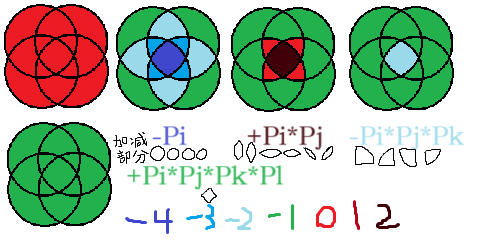
可得：

容斥原理
N-N/P₁-N/P₂-N/P₃-…-N/P_k
+N/P₁P₂+N/P₁P₃+…+N/P_k-1P_k
-N/P₁P₂P₃-…-N/P_k-2P_k-1P_k
+…
归纳得：

φ(N)=N(1-1/P₁)(1-1/P₂)(1-1/P₃)…(1-1/P_k)

代码

朴素做法

#include<bits/stdc++.h>
using namespace std;

const int N=105;

int res;
int n,a;
int prime[N];

int main(){
    cin.tie(0);
    cin>>n;
    while(n--){
        cin>>a;
        int res=a;
        for(int i=2;i<=a/i;i++){
            if(a%i==0){
                res=res/i*(i-1);
                while(a%i==0)a/=i;
            }
        }
        if(a>1)res=res/a*(a-1);
        cout<<res<<endl;
    }
    return 0;
}

线性筛法

前言

要是不会线性筛，就请先学一下先：
[编程笔记]-Prime_Basis质数基础

原理

特殊但不是很特殊地，φ(1)=1，因为1本身也与1互质。

当x为质数时，φ(x)=x-1

对于每个x=P_j*i：

1. 若i%P_j==0，那么P_j就是i的最小质因子，因此x的质因子就是i的质因子。所以，φ(x)=P_j*φ(i)。（详细：由于质因子相同，所以两个欧拉函数除了开头”N”部分都一样，而x也就是P_j*i，所以就是P_j*i*[函数后部分]，即P_j*φ(i)）
2. 若i%P_j!=0，那么P_j就不是i的质因子，但是i*P_j的最小质因子。因为P_j是质数，所以它的质因子只有它本身。φ(P_j*i)=P_j*i*[i的欧拉函数剩余部分]*(1-1/P_j)，也就等同于φ(P_j)*φ(i)，或者是(P_j-1)*φ(i)。

代码

int n, phi[N];

void euler(){
    int cnt=0;
    int prime[N];
    bool st[N]={false};
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!st[i]){
            prime[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;prime[j]<=n/i;j++){
            st[prime[j]*i]=true;
            if(i%prime[j]==0){
                phi[prime[j]*i]=prime[j]*phi[i];
                break;
            }
            phi[prime[j]*i]=phi[prime[j]]*phi[i];
        }
    }
}

欧拉定理

定理

若a与n互质，a^φ(n)≡1(mod n)

证明

若在1~n中，所有与n互质的数为a₁, a₂, …a_φ(n)

又因a与n互质，

所以a*a₁, a*a₂, …a*a_φ(n) 都满足≡1(mod n)

并且在这个序列里，产生的数两两各不相同。

证明如下：

反证法，若a*a_i≡a*a_j(mod n)
则a(a_i-a_j)≡0(mod n)
因a与n互质，可得：
a_i-a_j≡0(mod n)
a_i≡a_j(mod n)
但a_i, a_j都是n的不同的质因数，因此不成立。

因此，新序列也是φ(n)个互不相同且与n互质的数。

那么就可以得到（毕竟与n互质的数只有φ(n)个）：前后两个序列，内部元素（mod n后）其实是一样的，就是顺序可能会有所不同，所以它们乘积也应该同余。

那么易得：

a^φ(n)(a₁*…*a_φ(n))≡a₁*…*a_φ(n)(mod n)

又因a_i都是n的质因数，所以，(a₁*…*a_φ(n))也就是n的质因数。

所以a^φ(n)≡1(mod n)

别忘了a与n互质。

简单推论——费马小定理

当n为质数时，a^φ(p)≡1(mod p)

则，a^p-1≡1(mod p)

别忘了a与p互质。

没错这就是费马小定理。

完结撒花o(￣︶￣)o